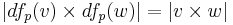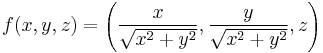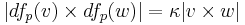Equiareal map

In differential geometry, an equiareal map is a smooth map from one surface to another that preserves the area of figures. If M and N are two surfaces in the Euclidean space R³, then an equi-areal map ƒ can be characterized by any of the following equivalent conditions:

The surface area of ƒ(U) is equal to the area of U for every open set U on M.
The pullback of the area element μ_N on N is equal to μ_M, the area element on M.
At each point p of M, and tangent vectors v and w to M at p,

$|df_p(v)\times df_p(w)|=|v\times w|\,$

where × denotes the Euclidean cross product of vectors and dƒ denotes the pushforward along ƒ.

An example of an equiareal map, due to Archimedes of Syracuse, is the projection from the unit sphere x² + y² + z² = 1 to the unit cylinder x² + y² = 1 outward from their common axis. An explicit formula is

$f(x,y,z) = \left(\frac{x}{\sqrt{x^2%2By^2}}, \frac{y}{\sqrt{x^2%2By^2}}, z\right)$

for (x,y,z) a point on the unit sphere.

In the context of geographic maps, a map projection is called equiareal, or more commonly equi-area, if areas are preserved up to a constant factor; embedding the target map, usually considered a subset of R², in the obvious way in R³, the requirement above then is weakened to:

$|df_p(v)\times df_p(w)|=\kappa|v\times w|\,$

for some κ > 0 not depending on $v$ and $w$ . For examples of such projections, see Equal-area map projections. Linear equi-areal maps are 2 × 2 real matrices making up the group SL(2,R) of special linear transformations.

References

Pressley, Andrew (2001), Elementary differential geometry, Springer Undergraduate Mathematics Series, London: Springer-Verlag, ISBN 978-1-85233-152-8, MR 1800436